Mit dem imc WAVE noise Analysator ermitteln Sie die akustischen Eigenschaften nach IEC 61672 Klasse 1 als zeitbewertender und integrierend Schallpegelmesser. Dabei lassen sich die Signale mehrerer Mikrofone parallel, online und synchron verarbeiten. Die Eigenschaften eines Kanals können von Hand aus dem Kalibrierblatt des Sensors eingegeben oder per TEDS-Chip automatisch eingelesen werden.
Da beim Messen nach Norm vor und nach jeder Messung eine Kalibriermessung des Mikrofons durchgeführt werden muss, ist dies eine zentrale Funktion in imc WAVE noise. Dabei kann der Messwert auf den angelegten akustischen Kalibrierwert justiert werden oder es wird einfach nur eine Kontrollmessung durchführt. Beide Verfahren werden mit dem Messkanal dokumentiert. Neben der Schallanalyse lässt sich das Mikrofonsignal im Oktav- oder Terzspektrum sowie als FFT-Analyse in Echtzeit berechnen und als 2D- oder 3D-Diagramm (Wasserfall) darstellen.
Als weitere Funktion steht Ihnen auch eine vollständige Schallleistungsmessung nach ISO 374x zur Verfügung.
Online Ergebnisse

- A-, B, -, C-, Z-Bewertungsfilter, Fast, Slow, Impuls, Peak und Leq
- Schallpegelmesser nach IEC 61672, IEC 60651 und IEC 60804
- 1/1-tel und 1/3-tel Oktavanalyse nach IEC 61260
- FFT Analyse (bis zu 131072 Punkte)
- Schallintensitätspegel mit Richtungs-Vorzeichen
- Schallintensitäts-Terzanalyse
- Schallintensitäts-FFT Analyse
Offline Ergebnis optional
- 1/12 Oktave und 1/24 Oktavband-Spektrum
- Lautheit und Lautheitsspektrum nach Zwicker ISO 532-1
- Sharpness bzw. Schärfe
- Artikulationsindex
Typische Anwendungen
- Normgerechte Akustikmessungen
- Abnahme- und Zertifizierungsmessungen in Zusammenhang mit Geräuschemission
- Produktqualifizierungen
- Produktoptimierungen im Entwicklungsbereich
- Geräuschkomfort in Fahrzeugen: Messungen zur Qualifizierung und Optimierung
- Ganzheitliche Untersuchungen zu Ursachen, Ausbreitungswegen und Auswirkungen von Schall und Schwingungen
- Einbringen von akustischer Expertise in allgemeinen Anwendungsbereichen von physikalischer Messtechnik
Wofür steht NVH?

NVH steht für: Noise - Vibration – Harshness
Der Mensch kann Schwingungen als Lärm (Noise) hören, als Schwingungen (Vibration) fühlen oder Rauhigkeit (Harshness) wahrnehmen. Dabei gehen die Phänomene auch ineinander über.
So spricht man von Vibrationen wenn Schwingungen im Frequenzbereich von ca. 0,1 Hz bis 20 Hz liegen. Diese können über unseren Körper wahrgenommen werden und das Wohlbefinden beeinflussen. Liegen diese Schwingungen im Frequenzbereich etwas höher, also von ca. 20 Hz bis 100 Hz, so dass die Schwingungen sowohl über unseren Körper spürbar, als auch über die Luft hörbar sind, spricht man von Rauhigkeit (Harshness). Da die spürbaren Schwingungen ab ca. 50-100 Hz deutlich abnehmen, spricht man im Frequenzbereich ab ca. 100 Hz bis 20 kHz von noise, also unangenehmen Luftschall den wir hören.
Was ist der Schallpegel?
Ein Schallpegelmesser ist ein Messsystem, das Geräusche ähnlich wie das menschliche Ohr erfasst. Es liefert also objektive und reproduzierbare Ergebnisse. Der Schallpegel sind Luftdruckänderungen im Frequenzbereich von 20 Hz bis 20 kHz, die mit einem Mikrofon erfasst und mit den entsprechenden Frequenz- und Zeit-Bewertungen analysiert werden. Diese Bewertungen und das Messverfahren ist in der DIN EN 61672 beschrieben. Hier spricht man von 2 Genauigkeitsklassen, Klasse 1 und Klasse 2, die aber in erster Linie von den verwendeten Mikrofonen abhängig sind.
Der Schallpegel wird immer in dB angegeben. Das schwächste Geräusch, das ein gesundes menschliches Ohr gerade noch hören kann, beträgt bei 1 kHz ca. 20 µPa.
Dies ist weniger als ein Milliardstel des normalen Luftdrucks, auf dem die Schallsignale überlagert sind. Um die Schmerzgrenze von Schalldruckschwankungen zu erreichen ist das Geräusch ca. 10 Millionen Mal größer, als die Hörschwelle. Um ein handlichen Maßstab des Schalls zu bekommen ist die dB-Skalierung eingeführt worden. Dabei entspricht der Faktor 10 im Schalldruck, eine Erhöhung des Pegels um 20dB.
Meist wird der Schallpegel mit einem in klammer stehenden Zusatz z.B. dB(A) beschriftet. Dabei steht das (A) für die Bewertung des Pegels. Es kann aber auch (B), (C) oder (D) in der Klammer stehen, wobei die B-Bewertung fast gar nicht mehr verwendet wird. Die C-Bewertung wird für impulshaltigen Lärm und die D-Bewertung bei Fluglärm eingesetzt.
Warum die dB-Skalierung?
Dies ist weniger als ein Milliardstel des normalen Luftdrucks, auf dem die Schallsignale überlagert sind. Um die Schmerzgrenze von Schalldruckschwankungen zu erreichen ist das Geräusch ca. 10 Millionen Mal größer, als die Hörschwelle. Um einen handlichen Maßstab des Schalls zu bekommen, wurde ist die dB-Skalierung eingeführt.
Dabei entspricht der Faktor 10 im Schalldruck, eine Erhöhung des Pegels um 20 dB. Das Dezibel ist keine Maßeinheit, sondern ein Verhältnis. Wie schon gesagt, ein Verhältnis zwischen einer gemessenen Größe in Pascal und der Hörschwelle von 20 µPa.
Meist wird der Schallpegel mit einem in Klammer stehenden Zusatz z.B. dB(A) beschriftet. Dabei steht das (A) für die Bewertung des Pegels. Es kann aber auch (B), (C) oder (D) in der Klammer stehen, wobei die B-Bewertung fast gar nicht mehr verwendet wird. Die C-Bewertung wird für impulshaltigen Lärm und die D-Bewertung bei Fluglärm eingesetzt.
Was ist die Frequenzbewertung?
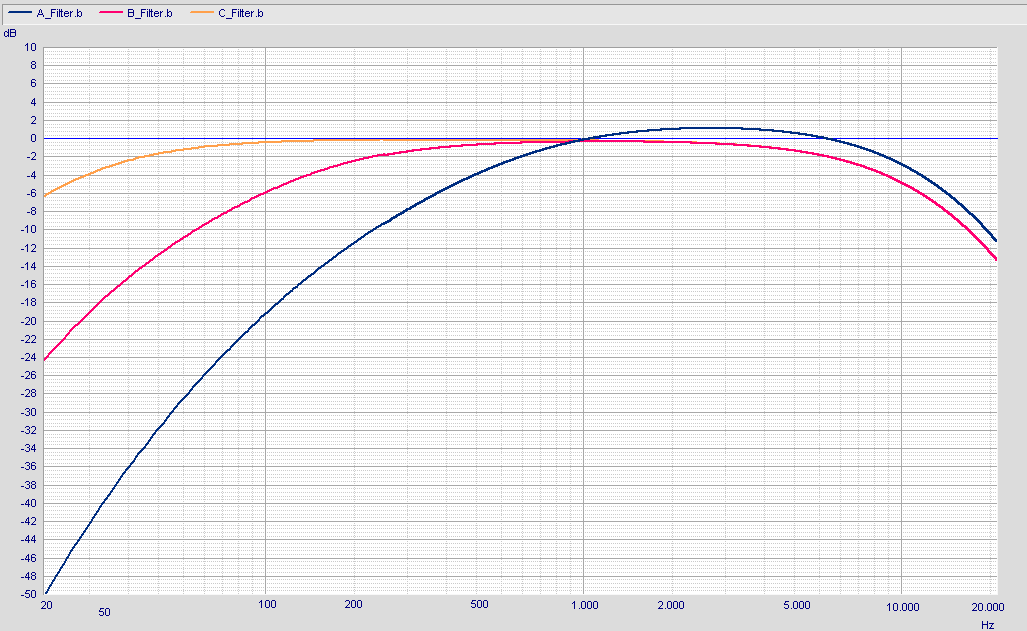
Es gibt vier Frequenz-Bewertungsfilter A, B, C oder Z.
A-Bewertung:
für niedrige Schallpegel ca. 20-40 Phone (blaue Kurve). Heutzutage wird mit der A-Bewertung fast ausschließlich gearbeitet. Dabei wird auf eine bessere Frequenzgangs-Anpassung zugunsten einer einfachen Handhabung, verzichtet.
B-Bewertung:
für mittlere Lautstärke ca. 50-70 Phone (rote Kurve). Heutzutage wird die B-Bewertung nicht mehr verwendet
C-Bewertung:
für hohe Schallpegel ca. 80-90 Phone (orange Kurve). Heutzutage wird die C-Bewertung auf dem Gebiet des Lärmschutzes für Zuschläge auf den A-Bewertungspegel herangezogen. Zuschläge nach TA-Lärm für impulshaltigen oder tonhaltigen Lärm.
Z-Bewertung:
bedeutet ohne Frequenzbewertung
Was ist die Zeit-Bewertung?
Die Zeit-Bewertung ermittelt den gleitenden Effektivwert des frequenzbewerteten Schall Signals. Sie ist ein Kompromiss zwischen schnellen folgen des schwankenden Schwingungssignals und der Ablesbarkeit des Messwerts und wird auch Anzeigeträgheit genannt.
FAST-Bewertung: Τ = 125 msec,
Beschreibung FAST: Schneller Anstieg und schneller Abfall des Signals.
Anstiegszeit nach T = 63% Abfallzeit nach T = 36% , Abfallzeit: -34,7 dB/sec
SLOW-Bewertung: Τ= 1000 msec
Beschreibung SLOW: Langsamer Anstieg und langsamer Abfall des Signals.
Anstiegszeit nach T = 63% Abfallzeit nach T = 36% , Abfallzeit: -4.3 dB/sec
IMPULSE-Bewertung: ΤAnstieg = 35 msec, TAbfall = 1500 msec,
Beschreibung IMPULSE: Sehr schneller Anstieg und sehr langsamer Abfall des Signals.
Anstiegszeit nach T = 63% Abfallzeit nach T = 36% , Abfallzeit: -2,9 dB/sec
Was ist eine Frequenzanalyse?
Eine Frequenzanalyse kann schmalbandig als FFT Analyse oder übersichtlich als Terz- und Oktav-Analyse berechnet werden.Bei der Frequenzanalyse wird grundsätzlich zwischen zwei Verfahren unterschieden: der Terz- und Oktavanalyse oder der FFT-Analyse.
Was ist eine Terz-/Oktavanalyse?
Um detaillierte Informationen über ein komplexes Schallsignal zu bekommen, müssen mehr Informationen über die Frequenzzusammensetzung des Signals ermittelt werden. Die unterschiedlichen Frequenzen lassen sich am einfachsten anhand der Tonleiter erklären.
Oktave [lat.], das Intervall, das vom Grundton 8 diatonalen Stufen entfernt ist, bezeichnet in der Akustik den Ton mit der doppelten Frequenz, bezogen auf einen Grundton. Seit der griechischen Antike geht die Darstellung des abendländischen Tonsystems von der Oktave aus. Die Terz-, Oktavanalyse (Terz [lat.], der dritte Ton) ist eine Frequenzanalyse mit relativ konstanter Frequenzauflösung, d. h., dass die Mittenfrequenz fm eines Bandpassfilters im Verhältnis zur Bandbreite (fB=fO-fU) für alle Frequenzbänder gleich ist. Die obere Eckfrequenz fO und die untere Eckfrequenz fU eines Frequenzbandpasses liegen bei einer Amplitudendämpfung von -3 dB (Faktor 0.707). Die relative Bandbreite der Oktave ist fB = 0.707, der Terz ist fB = 0,23 und der 1/12-tel-Oktave ist fB = 0,059.
Das Terz-/Oktavspektrum erlaubt eine Beurteilung der spektralen Leitungsverteilung, zum Beispiel eines Schallsignals. Sein Vorteil ist das logarithmische Frequenz-beurteilungsvermögen des menschlichen Ohrs. Die Terzfilter entsprechen in ihren Bandbreiten etwa den Frequenzgruppen, die das Unterscheidungsvermögen des Ohres erreichen. Deshalb haben sie für viele psychoakustische Probleme, auch für Lautheitsermittlung, eine ausreichende Trennschärfe.
Was ist eine FFT-Analyse?
Die Fast Fourier-Transformation (FFT) ist ein schneller Rechenalgorithmus zur Berechnung der diskreten Fourier-Transformation (DFT). Der von James Cooley und John W. Tukey (1965) entwickelte Algorithmus nutzt Rechenvorteile, die sich bei einer Anzahl von 2 hoch N Werten ergeben.

In modernen Analyse-Software Pakete ist man nicht mehr auf die Wertezahl von 2 hoch N angewiesen, denn ist die Anzahl der FFT-Punkte keine 2er Potenz, wird das Signal auf die entsprechend höhere Abtastfrequenz interpoliert.
So können mit imc WAVE verschiedene Parameter eingestellt werden.
- Frequenz Bewertung: A, B, C oder Z
- Mittelung: keine, Leq ab Start
- Fenster: Rechteck, Hamming, Hanning, Blackman Blackman-Harris und Flat-Top
- Überlappung: 0%, 10%, 25%, 33,33%, 50%, 66,66%, 75%, 90%
- Diff./Int.: differenzieren, zweifach differenzieren, integrieren, zweifach integrieren
- Punkte: 128…..131072
- Log.Achse: Ja / Nein
- Referenzwert dB 20 µPa = 2 E-05 Pa
- Anzeige von: Bandbreite, Auflösung und Ausgaberate